根据国家市场监督管理总局办公厅市监计量(2020)38号文件《市场监管总局办公厅关于下达2020年国家计量技术规范制定、修订及宣贯计划的通知》工作安排，《测量不确定度在法制计量合格评定中的作用》国家计量技术规范由全国法制计量管理计量技术委员会归口，已经完成了征求意见稿，现在面向全国公开充分征求意见。可下载征求意见稿相关材料，填写意见回执表，请您提出宝贵意见(填写在意见表中)，于2020年9月15日前将意见反馈给起草人邮箱。意见请反馈邮箱: 36555831@qq.com 或 cmqlixia@sina.com

       更多详情，请登录中国计量协会官方网站。

       节选该标准部分内容：

       范围

       本技术规范描述了测量不确定度在法制计量合格评定中的作用，即确定实体(产品、流程、体系、人员或机构)是否符合相关标准或规范的要求。本技术规范关注点是计量器具的合格评定，尤其关注于将测量或检定计量器具的测量结果作为法制计量合格评定的基础。例如定量包装的合格评定。

       本技术规范未涵盖的相关风险评估有：

       1) 抽样检测(例如损坏封印、标识等);

       2) 统计分析的计量器具总量;

       3) 净含量和定量包装的标识(参见 OIML R87 和 R79)。

       校准

       “测量单位”、“真值”、“测量误差”和“标准测量不确定度”的概念如图 A1 所示，图中右上角显示了测量(校准)一个标准砝码的情况。假设使用了一个高质量的测量系统(这里未提及也没有图示)来校准砝码。标准砝码的校准证书中包含了标准砝码的质量测得值(Mcalibrated)及相关的标准测量不确定度(ucalibrated)。在标准砝码的校准过程中，通过使用可溯源性原则获得标准测量不确定度或扩展不确定度(Ucalibrated)，并用横轴显示的测量基本单位表示。在图中右上角和横轴都标示了标准砝码的质量“真值”，且标注了这个“真值”是存在的，但从原理上来说是未知的。在横轴上标准砝码的质量“真值”附近有一对小垂线，表示由于“真值”定义不完整引入的不确定度。

       如 5.1 所述，图 A1 是一个概率密度函数(PDF)，提供了标准砝码质量“真值”位于某一个可能的“真值”附近无限小区域内的概率密度。根据概率密度函数可获得标准测量不确定度(ucalibrated)，通常用标准偏差表示，如图所示。

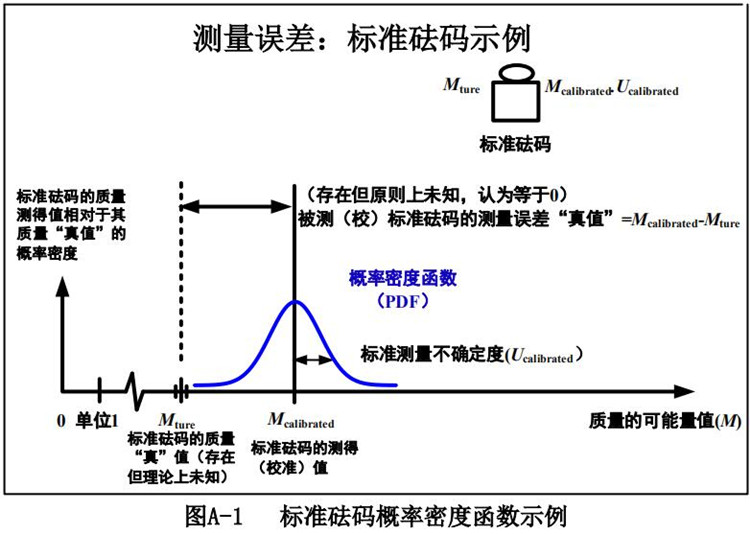
       图 A1 还显示了标准砝码质量 “测量误差”的“真值”，定义为标准砝码质量的测得值(校准值)与标准砝码质量的“真值”之差。需要注意的是，在图 A1 中由于标准砝码质量的“真值”是未知的，所以这个误差也是未知的。由于测量误差是未知的，所以 GUM 不鼓励使用误差的概念，而更愿意使用测量不确定度，因为测量不确定度是可以计算出来的，同时还能给出标准砝码质量真值为已知的置信水平。需要重点注意的是，测量时，尽管图A1 示出了可能的情况，但基于现有的测量(校准)信息，仍认为被测(校)标准砝码质量的测量误差真值为 0，因为所有已知的系统误差都能被修正。

       检定

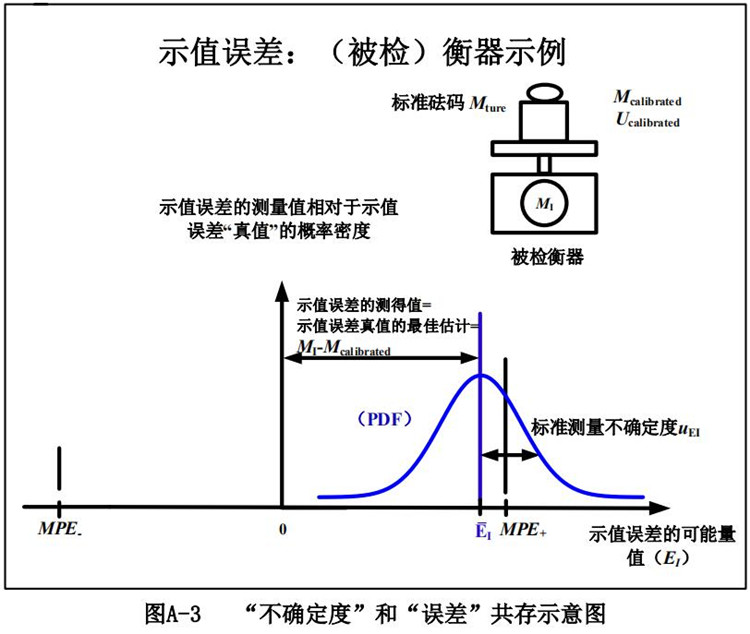
       如图 A2 所示，现在考虑用校准过的标准砝码来检定(不是校准)一个衡器。检定中，将被检衡器测得的标准砝码质量的示值与标准砝码本身的质量校准值进行比较。

       A2 包含的信息有很多与图 A1 相同，但增加了被检衡器测得的标准砝码质量的示值(MI)，还示出了“两个示值误差”：一个是相对于标准砝码质量“真值”的示值误差(未知)，另一个是相对于标准砝码质量测量(校准)值的示值误差(已知)。上文讨论过把计量标准装置(标准砝码)的质量测量(校准)误差“真值”视为零，因此在图 A2 中，示值误差测得值被认为是示值误差“真值”的“最 佳估计”。

       MPE 和测量不确定度

       确定计量器具恰当的最大允许误差(MPE)需要考虑测量不确定度。首次设置 MPE 时考 虑到可能的测量不确定度影响，可以降低与 MPE 相关的消费者、供应商或制造商的成本。 设置过小的 MPE 对仪器制造商而言是昂贵的代价，将不得不设计和构建更昂贵的计量标准 装置来满足严酷的检测要求，并且很可能会将额外的成本转嫁给消费者。考虑计量器具的 不同应用和用途，所涉及可能的测量不确定度水平，MPE 可设置得更具经济性，让步于可接受的风险水平。